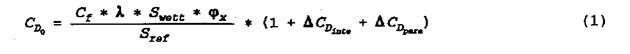3.3 AERODYNAMICS
The aerodynamic values can be estimated very precisely because they differ only by their Reynolds number. To value the aircraft, we need the diagram of the drag polar and the diagram of the lift
curve slope (CJa) .
3.3.1 The drag polar
The drag polar is the sum of the resistance factor at zero lift cdq, the coefficient of induced drag CDI and the resistance factor of compressible flow CDM.
CD = CD0 + CDI + CDM
where:
CDO = f (Re)
CDI = f(CL) and
CDM = f (Ma, CL) .
The theoretical zero lift drag is calculated by a method called “Group of Six-T-014J”
The formula for this calculation is:
- The skin friction drag coefficient was taken in the first 5% of the profile laminar. The rest of the aircraft has a turbulent flow.
- The form and sweep factors were taken for the wing, fuselage and pylons.
- For parasitic and interference drag, each was taken as 2.8% of the drag at clean flow around the airplane.
- The program for calculating the flight envelope (POP) adapts the values for different Mach numbers and heights by itself,
- varying the values of v/n
A detailed calculation of zero drag CDO at v/n= 7.22*106 1/m and the effect of the Reynolds number are in the appendix III.3.1.
The lift dependent drag CDI is calculated by the following formula from “HFP-R-300-PF2785, HORNER”:
The compressible drag is a super-critical drag 
which
consists of the wave drag and viscous effects, that follow the onset of transonic flow with local shocks. It is here defined by the locus in Mach number and lift coefficient for 
=0.002, also called M20. It is calculated with the “AI/TD 820.315/88” program.
The values for M20 were taken for the measurement of the A340, considering of the different sweep and the different relative wing thickness. The values for CDM were taken without changes for the higher Mach number. This is possible, if the Mach effects appear at higher Mach numbers.
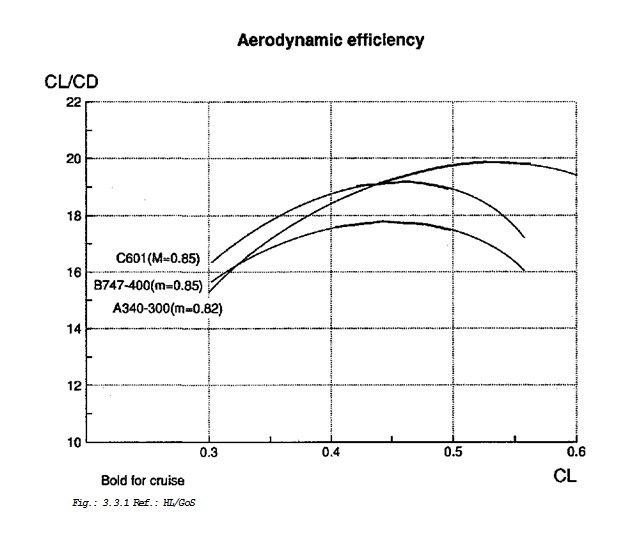
To have an impression of the performance, the CL/CD are shown at travelling conditions at a height of 10.7 km.
Fig.: 3.3.1 Ref.: HL/GoS
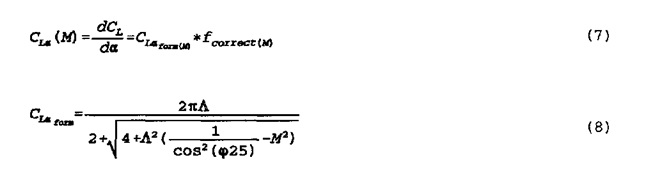
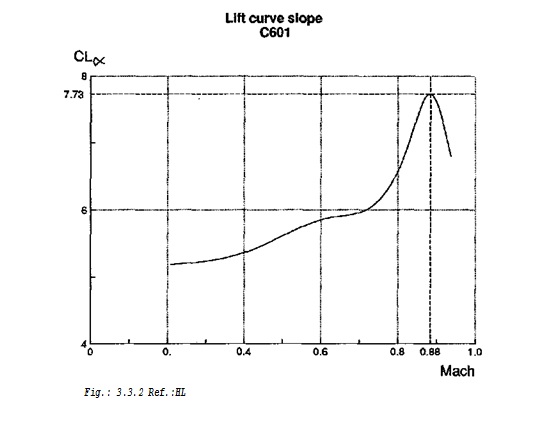
3.3.2 The lift curve slope
The lift curve slope ( CLa ) is calculated by the classical subsonic theory with a correction for transonic profiles
The correction factor relates to the necessary A340 correction factor between calculation and measured figures. A difference of 4% is added, because the wing is designed for a Mach number of 0.85 instead of Ma = 0.82 (see appendix III.3.2).
